13-гранна форма, відома як «капелюх», привертає увагу математиків.
Це перший справжній приклад «ейнштейна», єдиної форми, яка утворює особливу плитку площини: як плитка для підлоги у ванній кімнаті, вона може покривати всю поверхню без проміжків або накладень, але лише з візерунком, який ніколи не повторюється.
«Всі здивовані й раді, обидва», — каже математик Марджорі Сенечал зі Сміт-коледжу в Нортгемптоні, штат Массачусетс, яка не була причетна до відкриття. Математики півстоліття шукали таку форму. «Було навіть незрозуміло, що таке може існувати», — каже Сенешаль.
Хоча ім’я «Ейнштейн» нагадує про культового фізика, воно походить від німецького ein Stein , що означає «один камінь», і стосується однієї плитки. Ейнштейн сидить у дивному чистилищі між порядком і безладдям. Хоча плитки акуратно підходять одна до одної та можуть охоплювати нескінченну площину, вони аперіодичні, тобто не можуть утворювати візерунок, який повторюється.
Завдяки періодичному візерунку плитки можна пересунути, щоб вони ідеально відповідали попередньому розташуванню. Нескінченна шахова дошка, наприклад, виглядає так само, якщо пересунути рядки на два. Хоча можна розташувати інші одиничні плитки за візерунками, які не є періодичними, капелюх є особливим, оскільки він не може створити періодичний візерунок.

Визначений Девідом Смітом, непрофесійним математиком, який описує себе як «фантазії з уявою», і повідомив у статті, опублікованій 20 березня в Інтернеті на arXiv.org, капелюх — це полікіт — купа менших форм повітряних зміїв, склеєних разом. Це тип форми, який не вивчався уважно в пошуках Ейнштейна, каже Хаїм Гудмен-Штраус з Національного музею математики в Нью-Йорку, один із групи кваліфікованих математиків і комп’ютерників, з якими Сміт об’єднався для вивчення капелюх.
Це напрочуд простий багатокутник. До цієї роботи, якби ви запитали, як би виглядав Ейнштейн, Гудман-Стросс відповів: «Я б намалював якусь божевільну, звивисту, огидну річ».
Раніше математики знали про неповторювані плитки, які включали кілька плиток різної форми. У 1970-х роках математик Роджер Пенроуз виявив, що лише дві різні форми утворюють мозаїку, яка не є періодичною. Звідси виникло запитання: «Чи може існувати єдина плитка, яка це робить?» — каже математик Кейсі Манн з Вашингтонського університету Ботелла, який не брав участі в дослідженні. Його нарешті знайшли, «він величезний».
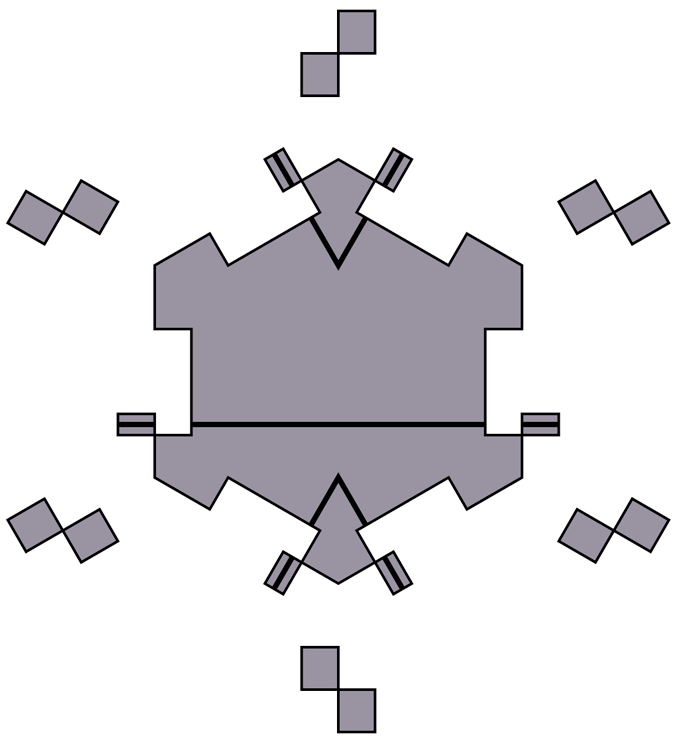
Інші форми наблизилися. Плитки Taylor-Socolar є неперіодичними, але вони являють собою набір із кількох від’єднаних частин — не те, що більшість людей думає про одну плитку. «Це перше рішення без зірочок», — каже математик Міхаель Рао з CNRS і École Normale Supérieure de Lyon у Франції.
Сміт і його колеги двома способами довели, що плитка була Ейнштейном. Один вийшов із того, що помітив, що капелюшки об’єднуються у більші кластери, які називаються метатилами. Потім ці метазаписи впорядковуються в ще більші суперзаписи, і так далі до нескінченності, у типі ієрархічної структури, яка є загальною для розрізів, які не є періодичними. Цей підхід показав, що черепиця капелюха може заповнювати всю нескінченну площину, і що її візерунок не повторюватиметься.
Другий доказ ґрунтувався на тому факті, що капелюх є частиною континууму форм: поступово змінюючи відносну довжину сторін капелюха, математики змогли сформувати сімейство плиток, які можуть мати однаковий візерунок, що не повторюється. Розглянувши відносні розміри та форми плиток у крайніх частинах цього сімейства — одна має форму шеврона, а інша нагадує комету — команда змогла показати, що капелюх не можна розташувати за періодичним візерунком.
Математики знайшли першого справжнього «Ейнштейна», схожу на капелюх фігуру, яку можна викладати, щоб охопити нескінченну площину, але з візерунком, який не може повторюватися. Капелюх є одним із сімейства споріднених плиток із багатьма різними формами. У цьому відео капелюхи перетворюються на різні форми. Порівнюючи крайні форми цього сімейства, одна у формі шеврона, а інша нагадує комету, дослідники змогли показати, що капелюх не може утворювати візерунок, який повторюється.
Хоча документ ще не пройшов рецензування, експерти, опитані для цієї статті, погоджуються, що результат, ймовірно, витримає детальне вивчення.
Шаблони, що не повторюються, можуть мати зв’язки з реальним світом. Вчений-матеріалознавець Ден Шехтман отримав Нобелівську премію з хімії 2011 року за відкриття квазікристалів , матеріалів з атомами, розташованими в упорядковану структуру, яка ніколи не повторюється, часто описуваних як аналоги мозаїкам Пенроуза. Нова аперіодична плитка може спровокувати подальші дослідження в матеріалознавстві, каже Сенешаль.
Подібні плитки надихали художників, і капелюх, здається, не виняток. Плитку вже художньо відтворили у вигляді усміхнених черепах і купи сорочок і капелюхів . Імовірно, це лише питання часу, коли хтось покладе плитку капелюха на капелюх.
І капелюх – це ще не кінець. Дослідники повинні продовжувати полювання на нових Ейнштейнів, каже комп’ютерний науковець Крейг Каплан з Університету Ватерлоо в Канаді, співавтор дослідження. «Тепер, коли ми відчинили двері, сподіваюся, з’являться інші нові форми».

